研究背景
虽然石墨烯基器件已被广泛用于从自然界获取各种能量,但用于能量获取的石墨烯片的波传播特性研究仍缺乏深入研究。
成果简介
澳大利亚莫纳什大学Wenhui Duan和东南大学Jian Zhang合作,以“Wave Propagation in Elliptic Graphene Sheet for Energy Harvesting”为题,在Nano Energy上发表最新研究成果,采用分子动力学模拟方法研究了椭圆石墨烯片的波传播,以实现高效的能量收集。研究发现,椭圆石墨烯片的能量收集效率优于三种长宽比的矩形石墨烯片,证明了椭圆石墨烯片在能量收集方面的优越性。考虑到能量收集时间和效率,纵横比为2的椭圆形石墨烯片具有最佳的动能收集效果。该研究发现将对设计和制造新兴的二维材料基能量采集器、质量传感器和气体探测器有极大地启发作用。
研究亮点
(1)首次研究了椭圆石墨烯在脉冲载荷下的波传播模式;
(2)通过施加正弦载荷,研究不同长宽比的椭圆石墨烯片的波传播速度;
(3)通过在不同位置施加线脉冲载荷,研究了椭圆单层石墨烯的波聚焦现象。
图文导读
1. 椭圆形石墨烯建模
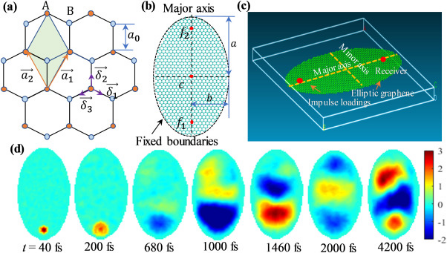
首先介绍了椭圆石墨烯片的概念,用于研究波传播、波聚焦和能量传输特性。石墨烯的蜂窝状网格结构如图1(a)所示。椭圆形石墨烯片的设计和示意图,如图1(b)和(c)所示。
椭圆形石墨烯片具有两个焦点(表示为f1和f2)和一个椭圆中心。在下面的模拟中,下焦点f1被设计为装载源位置,上焦点f2被认为是接收端。纵横比为1.5、2和2.5的椭圆形石墨烯片被建模和分析,以研究波聚焦和能量传输现象的差异。
在模拟中,在石墨烯片上施加了两种载荷,包括点载荷(施加在一个碳原子上)和线载荷(施加在一行中的几个碳原子上)。利用椭圆石墨烯片在点载荷作用下的动态位移,来研究波的传播和能量传输速度。此外,对椭圆石墨烯片在线载荷下的结果进行检验,研究能量收集应用中的波聚焦现象。
椭圆石墨烯片和动态模拟在Materials Studio进行,碳原子之间的相互作用通过COMPASS力场进行模拟。
2. 椭圆石墨烯片在点和线载荷下的波传播模式
2.1 点载荷
研究了椭圆石墨烯片在点和线载荷下的波传播模式。每种震源类型都考虑了两种类型的载荷,即脉冲冲击载荷和正弦载荷。确定了椭圆石墨烯片在正弦载荷下的波传播速度。更重要的是,对椭圆石墨烯片在线脉冲载荷下的波聚焦现象进行了广泛的研究,并研究了纵横比和加载位置对波聚焦和能量集中的影响,并与矩形石墨烯片进行了比较。
点脉冲载荷下纵横比为2的椭圆形石墨烯片的波传播结果如图1(d)所示。可以看出,位移波从40 fs到2000 fs向接收端传播,然后在到达固定边界时向后反射。位移波能量在到达石墨烯片的边界之前集中在下焦点(t = 200 fs,680 fs)。波能集中在位移大小相反的两个区域(t = 1460 fs),最终在下焦点、椭圆中心和上焦点(t = 2000 fs)周围形成三个集中区。当到达固定边界时,位移波发生后向反射,并在焦点和所研究的椭圆石墨烯片的椭圆中心周围,形成三个不同位移大小的能量集中区。
图1椭圆形石墨烯片的设计及示意图。(a)石墨烯的蜂窝点阵结构;(b)二维视图;(c)三维视图;(d)脉冲载荷下,所研究的石墨烯片的波传播模式。
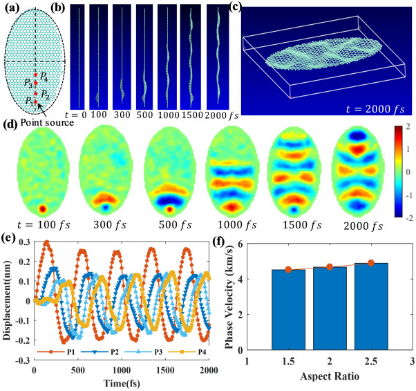
图2研究了椭圆石墨烯在点正弦载荷下的波传播。如图2(a)所示,椭圆石墨烯片在下焦点处受到周期为400 fs且振幅为10 km/s的点谐波速度。椭圆石墨烯在Y-Z平面正弦激发下的波传播过程(侧视图)如图2(b)所示,椭圆石墨烯在2000 fs时的三维变形图形如图2(c)所示。可以看出,位移波从所研究的石墨烯片的下焦点传播到上焦点。椭圆石墨烯在X-Y平面的位移波传播模式(俯视图)如图2(d)所示。正弦载荷下的椭圆石墨烯具有多个波聚焦区域,这些区域的数量取决于所施加载荷的频率值。然而,椭圆石墨烯在脉冲载荷下总是有两个/三个波聚焦区域。
纵横比为2的椭圆形石墨烯片,在不同位置的动态位移如图2(e)所示。不同纵横比的椭圆石墨烯的计算相速度如图2(f)所示。结果表明,随着石墨烯片长宽比的增加,相速度略有增加。
图2 点正弦载荷下,椭圆石墨烯的波传播(a)示意图;(b)模拟波传播的侧视图;(c)2000 fs时波传播模式的三维视图;(d)不同时间波传播模式的俯视图;(e)石墨烯片在不同位置的动态位移;(f)相速度。
2.2 线载荷
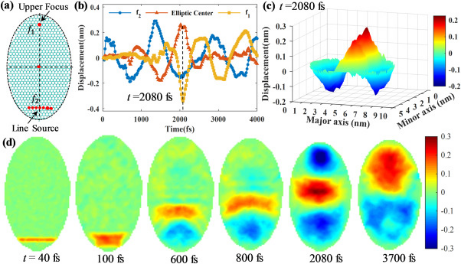
进一步研究了线载荷下,椭圆单层石墨烯片的波传播模式。图3显示了在线脉冲载荷下,纵横比为2的椭圆形石墨烯片的波传播结果。在下焦点周围施加大小为10 km/s的线脉冲冲击载荷,平行于椭圆形石墨烯片的水平轴(图3(a)),并且在椭圆形石墨烯的不同位置的振动位移在图3(b)中绘出。图3(c)给出了在2080 fs处,碳原子位移的三维表面图。可以看出,在该图中存在三个峰,两个峰在上下焦点处,具有负振幅,一个峰在椭圆中心处,具有正振幅。
椭圆石墨烯在不同时间的波传播模式如图3(d)所示。在40 fs处形成窄的矩形能量集中区,然后它作为梯形集中区(t=100 fs)传播。之后,位移波向前传播两个(t= 600 fs,800 fs)和三个不同的区域(t = 2080 fs)。当位移波到达固定边界时,波发生反射,能量集中在焦点(t = 3700 fs)和椭圆中心附近。
图3 线脉冲载荷下,椭圆石墨烯的波传播。(a)示意图;(b)动态位移;(c)2080 fs时动态位移的三维表面图;(d)不同时间的波传播模式。
3 高效能量收集的波聚焦
研究了线脉冲载荷下,纵横比对所研究的椭圆石墨烯片的波聚焦和能量输运的影响,并研究了加载位置(即平行于石墨烯片的垂直轴和水平轴)对波聚焦的影响。
3.1 纵横比的影响
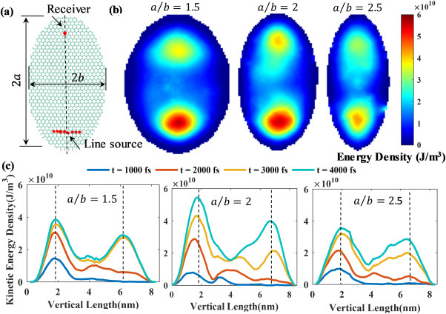
首次研究了椭圆石墨烯片在平行于短轴的线脉冲载荷作用下的波聚焦现象,具有不同纵横比的椭圆形石墨烯的结果如图4所示。在该研究中,在平行于具有三个纵横比的椭圆形石墨烯片的短轴的9个碳原子上,施加10 km/s量级的脉冲速度(图4(a))。
使用石墨烯片的模拟位移和振动频率来计算石墨烯片的动能密度Ek,不同纵横比的椭圆形石墨烯片的空间能量分布如图4(b)所示。可以看出,动能集中在具有三个纵横比的椭圆石墨烯的下焦点和上焦点。图4(c)提取并比较了不同时间沿主轴的动能密度。三个不同长宽比的椭圆形石墨烯片呈现两个不同的峰,表明动能可以在石墨烯片的两个焦点处获得。纵横比为2的椭圆形石墨烯片的动能密度在三个椭圆形石墨烯片中具有最高的能量峰值。因此,优化椭圆形石墨烯片的纵横比对于获取最大的能量是极为重要的。
图4 不同长径比椭圆石墨烯片的能量聚焦。(a)加载条件示意图;(b)空间能量分布;(c)沿主轴的时变动能密度。
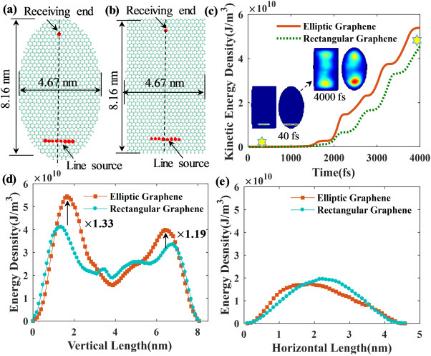
此外,还比较了椭圆形石墨烯片和矩形石墨烯片的能量聚焦现象。纵横比为2的矩形和椭圆形石墨烯片的能量聚焦的结果如图5所示。作用在矩形石墨烯片上的线脉冲载荷(图5(b))保持与作用在椭圆形石墨烯片上的线脉冲载荷相同(图5(a))。图5(c)绘出了接收端的计算动能,以研究能量集中现象。在0 fs到4000 fs范围内,椭圆石墨烯在接收端的动能大于矩形石墨烯。在4000 fs时,与矩形石墨烯相比,椭圆形石墨烯片具有两个不同的能量集中区域。为了验证这一现象,提取了沿着椭圆形和矩形石墨烯板的主轴的动能密度(如图5 (d)所示)。可以看出,椭圆形石墨烯片上下焦点处的动能密度分别是相应矩形石墨烯片的1.33倍和1.19倍。可以得出结论,与矩形石墨烯相比,椭圆形石墨烯片可以在焦点处获得更多的能量。这一现象证明了椭圆形石墨烯片比矩形石墨烯片更适合能量收集。
图5 线冲击加载源下,矩形和椭圆形石墨烯片的波聚焦比较。(a)椭圆形石墨烯的加载条件;(b)矩形石墨烯的加载条件;(c)接收端的能量演化曲线;(d)沿垂直轴的能量密度;(e)沿水平轴的能量密度。
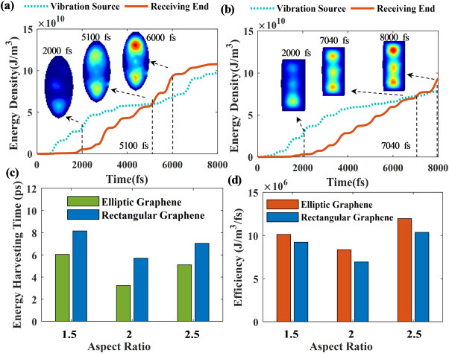
此外,为了说明能量收集效率,提取并比较了椭圆石墨烯和矩形石墨烯在不同时间的动能。在该研究中,在下焦点周围施加线脉冲加载源,纵横比为2.5的椭圆形和矩形石墨烯片的时变能量密度如图6所示。结果表明,相对于矩形石墨烯片,椭圆形石墨烯片可以在短时间内在接收端获得与加载位置相同的能量。结果表明,相对于矩形石墨烯片,椭圆形石墨烯片可以在短时间内在接收端获得与加载位置相同的能量。
图6(c)进一步比较了椭圆形和矩形石墨烯片的能量收集时间。可以看出,纵横比为2的矩形石墨烯片的能量收集时间在三个纵横比中是最低的,其次是纵横比为2.5和1.5的石墨烯片,这个现象和椭圆形石墨烯片是一样的。矩形石墨烯片和椭圆形石墨烯片的区别在于,椭圆形石墨烯片收获相同能量所需的时间比矩形石墨烯片少。此外,图6(d)计算了矩形和椭圆形石墨烯片的能量收集效率。研究发现,椭圆石墨烯片的能量收集效率优于三种长宽比的矩形石墨烯片,证明了椭圆石墨烯片在能量收集方面的优越性。
图6 石墨烯片能量收集效率的比较。(a)椭圆形石墨烯片的能量密度演化;(b)矩形石墨烯片的能量密度演化;(c)能量收集时间;(d)能量收集效率。
3.2 加载位置的影响
进一步研究了椭圆石墨烯片在不同加载位置下的波聚焦现象和能量输运。为了研究加载位置对波聚焦现象的影响,在椭圆石墨烯片的右中部和右下部施加了线脉冲加载。
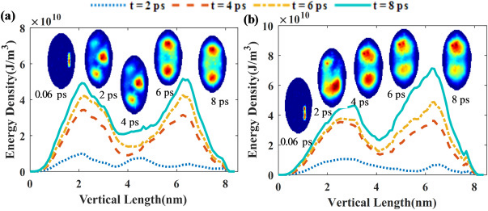
纵横比为2的椭圆形石墨烯片的能量传输结果如图7所示。图7(a)显示了当线脉冲载荷位于右中心部分时,沿垂直轴的动能密度的演变。可以看出,开始时动能集中在石墨烯片的右中央部分。它传播到下焦点(t = 2 ps,4 ps),最后聚焦在上下焦点(t = 6 ps,8 ps)。椭圆石墨烯的这种能量传输路径与右下部分应用线脉冲加载时的结果相同(图7(b))。
图7 加载位置对长宽比为2的椭圆石墨烯片波聚焦和能量输运的影响。(a)加载作用在石墨烯片的右侧;(b)加载作用在石墨烯片的右下方。
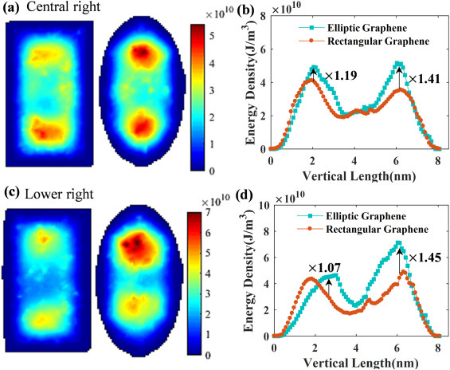
将线加载源位于不同位置时,椭圆形石墨烯的动能分布与矩形石墨烯进行比较(图8)。图8(a)和图8(c)示出了不同加载位置下椭圆形和矩形石墨烯片在8 ps时的空间能量分布。可以看出,与相应的矩形石墨烯相比,无论在哪里施加线冲击载荷,椭圆形石墨烯片都具有两个不同的能量集中区域,并且更多的能量倾向于集中在椭圆形石墨烯片,而不是矩形石墨烯片的上下焦点处。
图8(b)和(d)表明,椭圆形石墨烯片比矩形石墨烯片能收获更多的能量,同时也证明了无论线载荷在哪里作用,动能都趋向于集中在椭圆石墨烯片的焦点上。
图8 矩形和椭圆形石墨烯片的能量收集比较。(a)当线脉冲载荷施加在右中心部分时的空间能量分布;(b)沿主轴的能量密度;(c)在右下方施加线脉冲载荷时的空间能量分布;(d)沿主轴的能量密度;
结论
石墨烯片已被广泛用于利用波传播特性,设计纳米谐振器和吸收器。然而,椭圆石墨烯片的波传播模式和能量输运尚未得到研究。本文通过分子动力学模拟方法,研究了椭圆石墨烯片在不同加载条件和几何参数下的波传播、波聚焦和能量输运行为。本文的研究结果对能量采集器的设计和制造有一定的参考价值。。
文献链接
Wave Propagation in Elliptic Graphene Sheet for Energy Harvesting (Nano Energy, 2021, DOI: 10.1016/j.nanoen.2021.106089)
原文链接:https://doi.org/10.1016/j.nanoen.2021.106089